GloVe 论文笔记
关于 EMNLP'14 论文《GloVe: Global Vectors for Word Representation》的阅读笔记
GloVe 介绍
GloVe 来源于论文《GloVe: Global Vectors for Word Representation》,由 Stanford 的 Jeffrey Pennington 发表在 EMNLP 2014 上。GloVe 研究的任务是把自然语言单词转换为计算机易于处理的表示形式,比如一维向量。GloVe 其实就是全局向量的意思,它是一个词向量模型,并且利用了统计好的全局信息,其类似的方法包括 one-hot、Word2Vec( CBOW & Skip-Gram )等。
GloVe 研究动机
- 传统的基于全局统计的方法,比如 SVD,不能迭代训练,性能不高
- 基于深度学习和上下文窗口的方法,比如 Word2Vec,只对小窗口内的上下文建模,忽略了全局信息
- GloVe,想利用全局统计信息,并且可以训练(以机器学习方式,没有使用神经网络)
GloVe 引入:如何表示两个词的相似性
词向量的相似性计算
如果我们得到了词向量,可以用向量的距离度量判断两个词是否相似(余弦距离/曼哈顿距离/欧式距离)
共现矩阵
如何基于全局统计信息来度量两个单词是否相似?
- GloVe 首先统计出共现矩阵 \(X_{ij}\),表示单词 \(j\) 在单词 \(i\) 附近(比如5个词内)出现的次数
- 共现矩阵 \(X\) 每一行的和 \(X_{i}\) 表示整个语料库一共有多少单词出现在单词 \(i\) 附近
- 共现概率 \(P_{ij}=P(j|i)=\frac{X_{ij}}{X_{i}}\) 表示单词 \(j\) 出现在单词 \(i\) 附近的概率
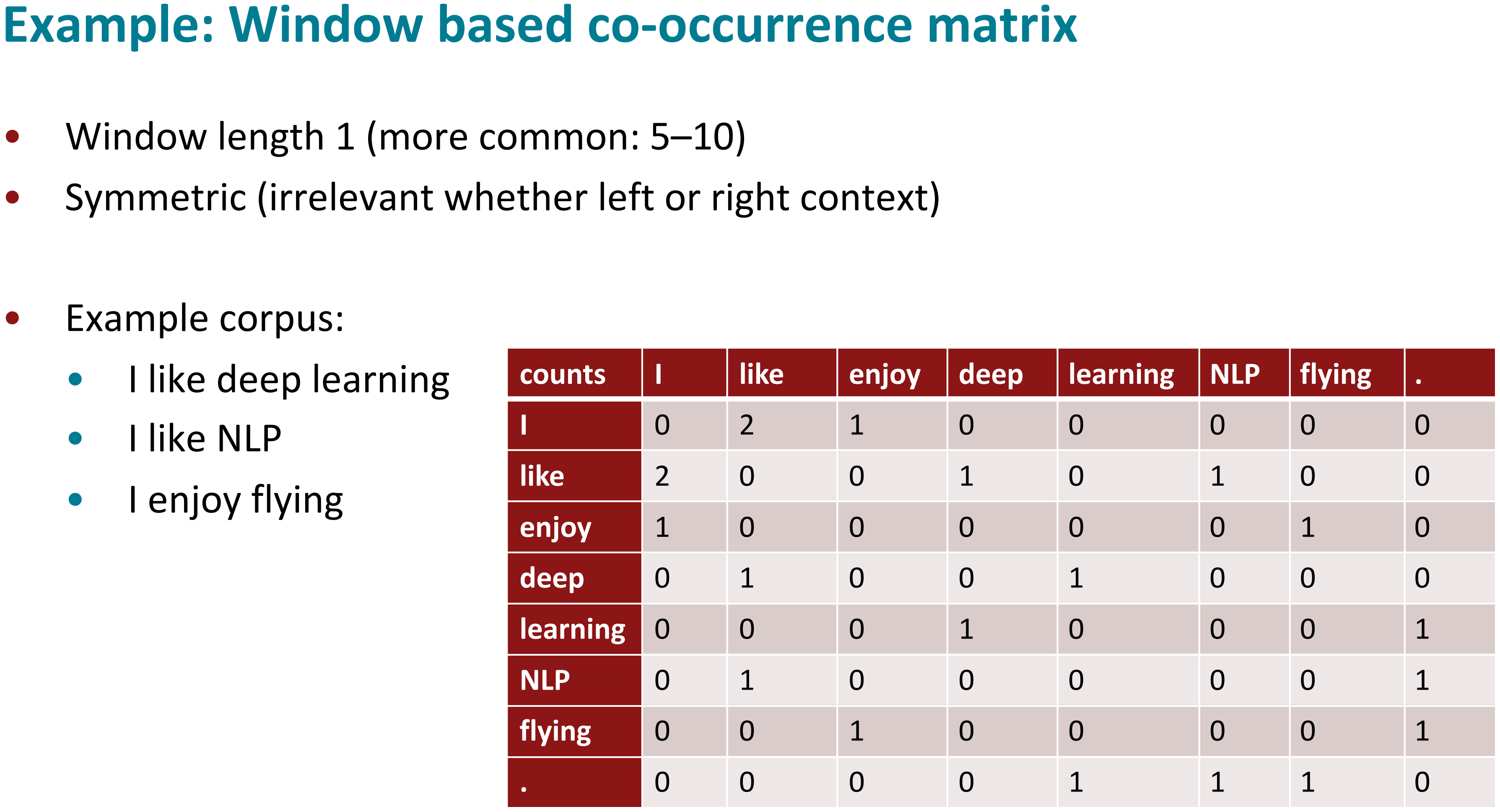
从上面的图可以看出,\(X_{I,like}=2\),\(X_{I}=3\),\(P_{I,like}=2/3\)
我们注意到在共现矩阵中 \(X_{ij}=X_{ji}\)(即 \(X=X^T\)),也就是中心词 \(i\) 和背景词 \(j\) 的角色可以任意互换
利用共现矩阵表示两个单词的相似性
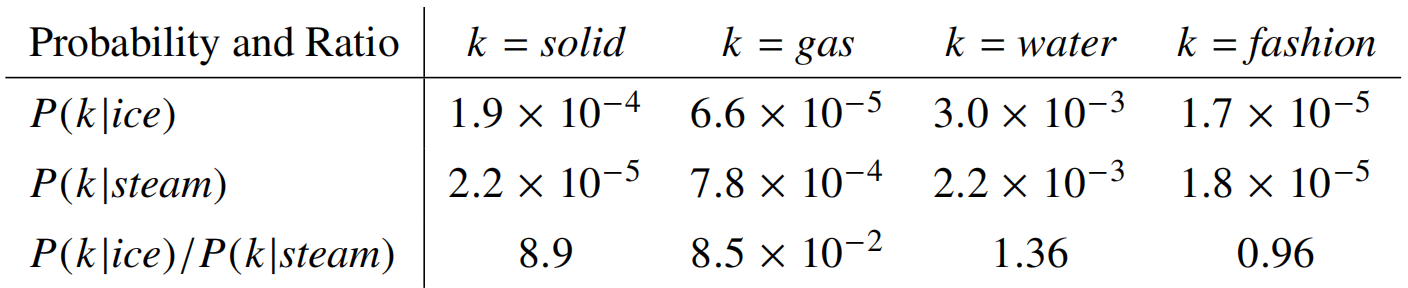
- 已知单词 \(i\) 和单词 \(j\),现在有一个单词 \(k\),如何判断单词 \(k\) 距离单词i近,还是单词 \(j\) 近?
- 可以用共现概率的比值来确定:\(\frac{P_{ik}}{P_{jk}}\)
- 比值大于1表明 \(k\) 与 \(i\) 近;比值小于1表明 \(k\) 与 \(j\) 近;比值等于1说明和 \(i\)、\(j\) 距离相似(都比较接近或都没什么关系)
GloVe 建模:构建模型
因为 \(\frac{P_{ik}}{P_{jk}}\) 可以表示 \(k\) 与 \(i\) 和 \(j\) 之间的相似度关系,所以想办法构建函数 \(F\),使得对于表示单词 \(i\)、\(j\)、\(k\) 的向量 \(w_i\)、\(w_j\)、\(\tilde{w}_k\) 与 \(\frac{P_{ik}}{P_{jk}}\) 建立联系
\[ F(w_i,w_j,\tilde{w}_k)=\frac{P_{ik}}{P_{jk}} \]
\(w\) 表示中心词,\(\tilde{w}\) 表示背景词
通过以下假设与限制,从抽象的 \(F\) 设计出一个具体的 \(F\) 函数
- \(F\) 表达的含义和形式应该和 \(\frac{P_{ik}}{P_{jk}}\) 一致
- 中心词 \(i\) 可以是任意的,\(i\) 和 \(k\) 的角色互换,公式表达的含义不变
GloVe 模型不是推导出来的,是作者的一种设计!
- \(F\) 表达的意义和形式应该和\(\frac{P_{ik}}{P_{jk}}\)一致
- \(\frac{P_{ik}}{P_{jk}}\) 表示单词之间的距离度量,这可以用向量之差表示
- \(\frac{P_{ik}}{P_{jk}}\) 是标量,可以用向量内积来进行转换
\[ F \left((w_i-w_j)^{T}\tilde{w}_k \right)=\frac{P_{ik}}{P_{jk}} \tag{1} \label{eq1} \]
直观上可以用余弦相似度简单理解这么设计的合理之处
- 中心词 \(i\) 可以是任意的,\(i\) 和 \(k\) 的角色互换( \(w\) 和 \(\tilde{w}\)、共现矩阵 \(X\) 和 \(X^T\) ),公式表达的含义不变,这需要如下一系列设计
首先公式 \(\ref{eq1}\) 肯定不满足上述要求,交换 \(i\) 和 \(k\),无论公式的左边和右边都和原来不想等。我们通过观察可以发现主要是 \(j\) 的存在让公式无法满足这种对称性,我们可以先办法把 \(j\) 去掉,作者进行了如下构造
\[ F \left((w_i-w_j)^{T}\tilde{w}_k \right)=F (w_i^{T}\tilde{w}_k-w_j^{T}\tilde{w}_k)=\frac{F(w_i^{T}\tilde{w}_k)}{F(w_j^{T}\tilde{w}_k)}=\frac{P_{ik}}{P_{jk}} \tag{2}\label{eq2} \]
指数函数满足 \(F\) 的性质,不妨假设 \(F\) 为指数函数,即 \(F(x)=e^x\),由公式 \(\ref{eq2}\),可以得到
\[ F(w_i^{T}\tilde{w}_k)=e^{w_i^{T}\tilde{w}_k}=P_{ik}=\frac{X_{ik}}{X_i} \tag{3} \]
所以
\[ w_i^{T}\tilde{w}_k=\log \left (\frac{X_{ik}}{X_i}\right )=\log (X_{ik}) - \log (X_i) \tag{4} \]
此时有
\[ w_i^{T}\tilde{w}_k +\log (X_i) =\log (X_{ik}) \tag{5} \]
\(\log (X_i)\) 与 \(k\) 无关,我们可以用 \(b_i\) 来拟合它
\[ w_i^{T}\tilde{w}_k + b_i =\log (X_{ik}) \tag{6} \]
此时公式左侧再加上 \(\tilde{b}_k\),就可以满足这种对称性( \(i\) 和 \(k\) 互换,公式的左边和右边都和原来相等!)
\[ w_i^{T}\tilde{w}_k + b_i + \tilde{b}_k =\log (X_{ik}) \tag{7} \label{7} \]
注意向量内积是满足交换律的,即 \(w_i^{T}\tilde{w}_k=w_k^{T}\tilde{w}_i\),并且有 \(X_{ik}=X_{ki}\)(由共现矩阵的性质)
这时我们就构建好了模型,用 \(w_i^{T}\tilde{w}_k + b_i + \tilde{b}_k\) 来拟合 $(X_{ik}) $(已知量),即全局对数双线性回归模型
我们可以得到两组词向量 \(w\) 和 \(\tilde{w}\),它们应该是等价的,作者把 \(w+\tilde{w}\) 作为 GloVe 最终的词向量
GloVe 损失函数
GloVe 使用均方差损失函数,即 \[ J=\sum\limits_{i,j=1}^{V}(w_i^{T}\tilde{w}_k + b_i + \tilde{b}_k-\log (X_{ik}))^2 \]
考虑到共现次数少的词对携带信息量少,并且共现次数为0时 \(\mathrm{log()}\) 无法计算。在损失函数中添加一个关于共现次数 \(X_{ij}\) 的权重函数 \(f(X_{ij})\),损失函数变为
\[ J=\sum\limits_{i,j=1}^{V}f(X_{ij})(w_i^{T}\tilde{w}_j + b_i + \tilde{b}_j-\log (X_{ij}))^2 \]
这里把 \(k\) 变成 \(j\),是为了和原文一致,公式表达的意思都是一样的
\(f(X_{ij})\) 应满足如下性质
- \(f(0)=0\)
- \(f\) 是非减函数,即共现次数越多权重越大(或不变)
- 对共现次数特别大的词对,\(f\) 不是特别大
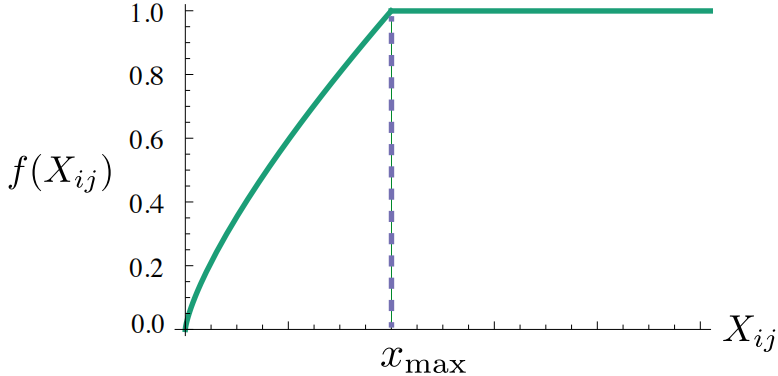
作者最终选择如下的 \(f\)
\[ f(x)=\left\{ \begin{aligned} & (x/x_{\max})^\alpha \quad \mathrm{if} \;\, x< x_{\max} \\ & 1 \quad \mathrm{otherwise} \quad \mathrm{.} \end{aligned} \right. \]
其中 \(x_{\max}\) 是设置的共现次数的阈值,作者根据语料库统计设置为 100,\(\alpha\) 是超参数,作者根据实验效果设置为 0.75
GloVe 实验结果
单词类比
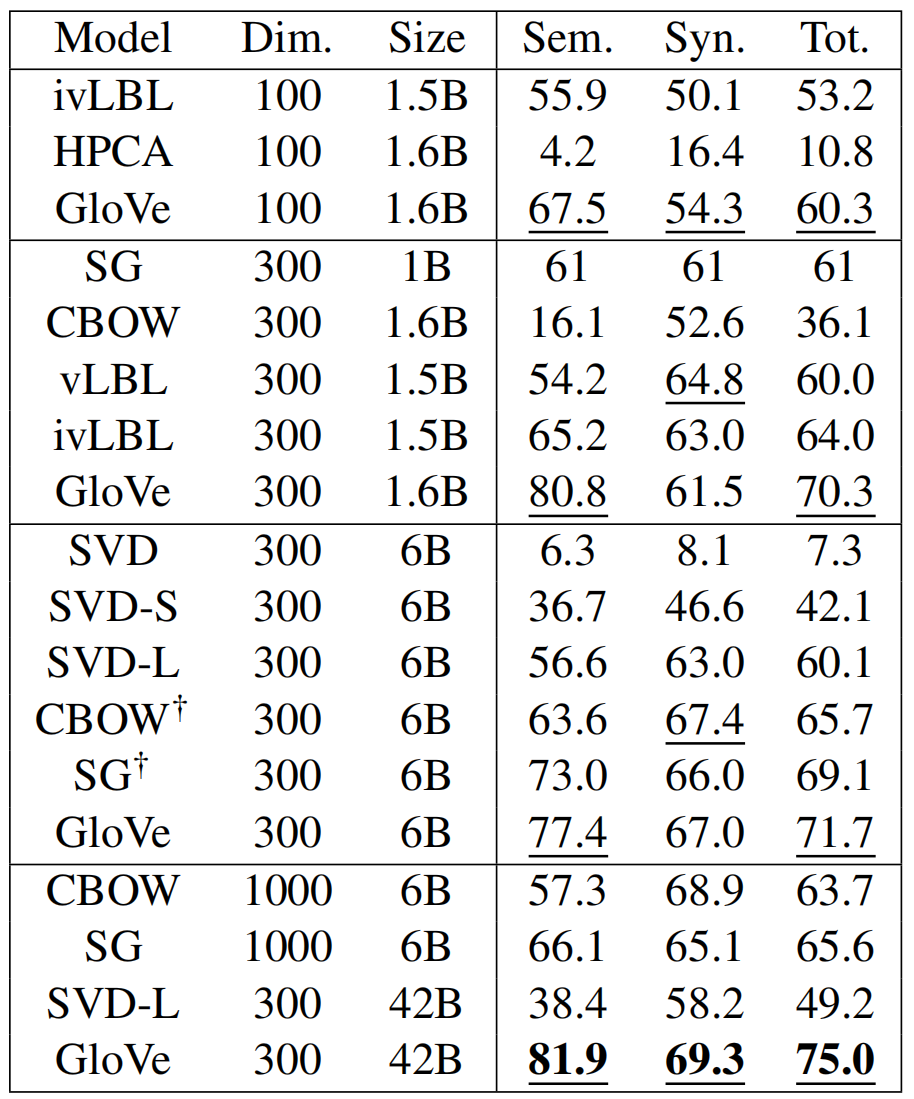
- 单词类比:爸爸和妈妈类比儿子和女儿
- Dim:词向量的维度;Size:语料库大小,6B 表示有6 billion tokens
单词相似度
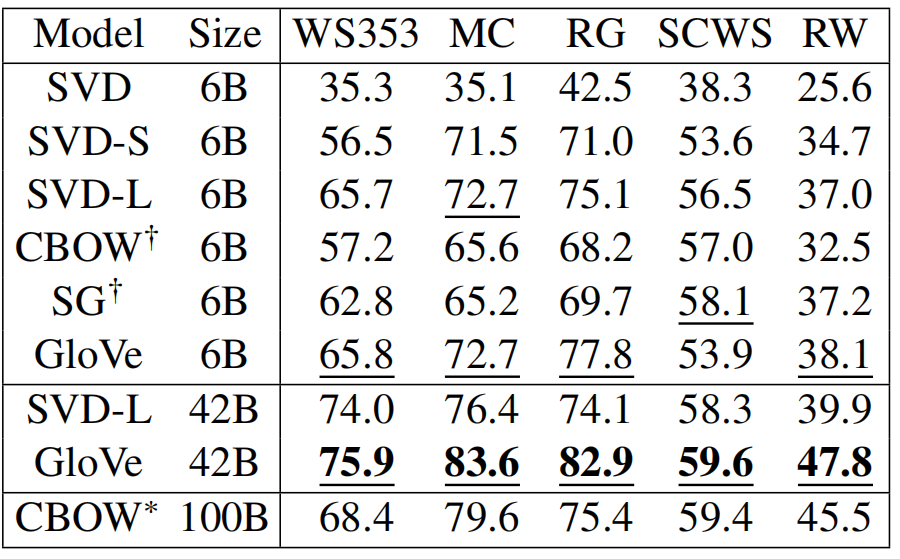
- 单词相似度:哪一个词和爸爸的意思最接近?父亲、母亲、爷爷、奶奶
- GloVe 42B 比 Word2Vec 100B 效果还好
命名实体识别
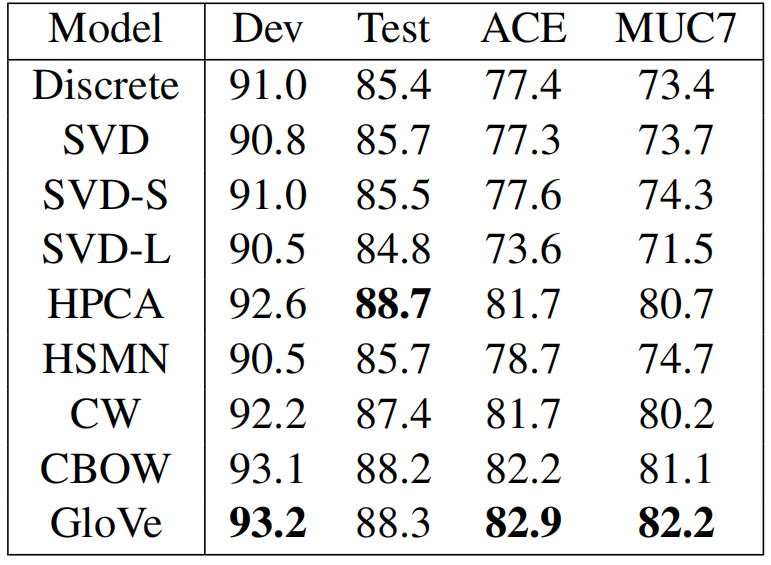
- 命名实体识别( NER ):识别出一句话内的人名、地点、组织等信息。特朗普是美国人
- NER模型类似 FFN+CRF(序列标注模型),把词向量作为特征输入到 FFN,FFN 的输出作为 CRF 的发射概率
- 在下游任务上,GloVe的优势不明显
总结
GloVe 与 Word2Vec 是最流行的非 BERT 类词向量模型,我个人认为二者性能相似,具体用哪个可以先根据自己的任务测试一下。我不认同“GloVe 使用了全局信息因此比Word2Vec效果要好”的观点,GloVe 论文最后一节的推导了实际上说明 GloVe 与 Skip Gram 是等价的;我也不认同“GloVe 使用了共现概率比因此比Word2Vec效果要好” 的观点,在 GloVe 模型推导的中途为了满足对称性实际上抛弃掉了比的形式。由公式 \(\ref{7}\) 直观的理解,GloVe实际上就是让共现次数多的两个词的词向量的内积大。不过我们可能凭空想不出来这个公式,因此作者前面给出了设计这个公式的思路。用计算语言学课上钱老师的话讲,“共现次数可能是比较大的值,因此加一个 \(\mathrm{log}\) 函数让量纲变的一致”。